| Date and Time (Pacific) |
Speaker |
Title |
| April 3, 4 pm |
Will Sawin (Columbia) |
The Shafarevich conjecture for hypersurfaces in abelian varieties (abstract) |
| April 17, 11-12:30 |
Gavril Farkas (Humboldt) |
Green’s Conjecture via Koszul modules |
| April 24, 11-12:30 |
Kirsten Wickelgren (Duke) |
There are 160,839 + 160,650 3-planes in a 7-dimensional cubic hypersurface (video) |
| May 1, 10:45-11:45 |
Borys Kadets (MIT) |
38406501359372282063949 & all that: Monodromy of Fano Problems |
| May 1, 12-1 |
Burt Totaro (UCLA) |
The Hilbert scheme of infinite affine space |
| May 8, 10:45-11:45 |
Julie Desjardins (Toronto) |
Density of rational points on a family of del Pezzo surface of degree 1 (slides) |
| May 8, 12-1 |
Bjorn Poonen (MIT) |
Bertini irreducibility theorems via statistics |
| May 15 10:45-11:45 |
Rohini Ramadas (Brown) |
The locus of post-critically finite maps in the moduli space of self-maps of 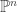 |
| May 15, 12-1 |
Rob Silversmith (Northeastern) |
Studying subschemes of affine/projective space via matroids |
| May 22, 11-12:30 |
Chenyang Xu (MIT) |
K-moduli of Fano varieties |
| May 29, 10:45-11:45 |
Yuchen Liu (Yale) |
Moduli spaces of quartic hyperelliptic K3 surfaces via K-stability (slides) |
| June 5, 12-1 |
Bhargav Bhatt (Michigan) |
A p-adic Riemann-Hilbert functor and vanishing theorems |
| June 12, 10:45-11:45 |
Margaret Bilu (NYU) |
Arithmetic and motivic statistics via zeta functions (video) |
| June 12, 12-1 |
Wei Ho (Michigan) |
Splitting Brauer classes (slides) |
| July 10, 12-1 |
John Christian Ottem (Oslo) |
On (2,3)-fourfolds (video, slides)
|
| July 17, 12-1 |
Laura Escobar Vega (Washington University St. Louis) |
Wall-crossing phenomena for Newton-Okounkov bodies (video, slides) |
| July 24, 12-1 |
Brendan Hassett (Brown/ICERM) |
Symbols, birational geometry, and computations (video, slides) |
| July 31, 12:30-1:30 |
Dan Abramovich (Brown) |
Resolution and logarithmic resolution via weighted blowings up (video, slides) |
| August 21 |
Hannah Larson (Stanford) |
Brill–Noether theory over the Hurwitz space (slides)
|
| August 28 |
Martin Olsson (Berkeley) |
Determinants and deformation theory of perfect complexes (video, slides)
|
| September 4 |
Christopher Eur (Stanford) |
Simplicial generation of Chow rings of matroids (slides) |
| September 11 |
Andrew Kobin (Santa Cruz) |
Zeta functions and decomposition spaces (video, slides) |
| September 18 |
Rachel Webb (Berkeley) |
Virtual cycle on the moduli space of maps to a complete intersection (slides)
|
| September 25 |
Richard Thomas (Imperial College London) |
Square root Euler classes and counting sheaves on Calabi-Yau 4-folds (video, slides)
|
| October 2 |
Juliette Bruce (Berkeley) |
The top weight cohomology of 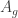 (video, slides) (video, slides) |
| October 9 |
Karen Smith (University of Michigan) |
Extremal Singularities in Prime Characteristic (video)
|
| October 16 |
Barbara Fantechi (SISSA, Italy) |
Infinitesimal deformations of semi-smooth varieties (video)
|
| October 23 |
Jarod Alper (University of Washington) |
Coherent completeness and the local structure of algebraic stacks (video)
|
| October 30 |
Aaron Landesman (Stanford) |
The Torelli map restricted to the hyperelliptic locus (video)
|
| November 6 |
Akhil Mathew (University of Chicago) |
Etale K-theory and motivic cohomology (video, slides)
|
| November 13 |
Taylor Dupuy (University of Vermont) |
Abelian Varieties Over Finite Fields in the LMFDB (video, slides)
|
| December 4 |
Rahul Pandharipande (ETH Zurich) |
The top Chern class of the Hodge bundle and the log Chow ring of the moduli space of curves (video, slides)
|