(The seminar webpage is here.)
Sam Grushevsky (Stony Brook University)
September 29, 2017
Geometry of compactified moduli of cubic threefolds
Starting from considering the GIT compactification of the moduli of cubic threefolds, the “wonderful” compactification, which is smooth with normal crossing boundary, is constructed by an explicit sequence of blowups. We show that there exists a family of intermediate jacobians over the wonderful compactification. We compute the cohomology of the wonderful compactification by comparing it to the symplectic resolution. Based on joint works with Casalaina-Martin, Hulek, Laza
Felix Janda (University of Michigan)
October 6, 2017
Genus two curves on quintic threefolds
Virtual (Gromov-Witten) counts of maps from algebraic curves to quintic 3-folds in projective space have been of significant interest for mathematicians and physicists since the early 90s. While there are (very inefficient) algorithms for computing any specific Gromov-Witten invariant, explicit formulae are only known in genus zero and one. On the other hand, physicists have explicit conjectural formulas up to genus 51.
I will discuss a new approach to the Gromov-Witten theory of the quintic (using logarithmic geometry) which yields an explicit formula in genus two that agrees with the physicists’ conjecture.
This is based on joint works in progress with Q. Chen, S. Guo and Y. Ruan.
Remy van Dobben de Bruyn (Columbia)
October 20, 2017
Dominating varieties by liftable ones
Given a smooth projective variety over an algebraically closed field of positive characteristic, can we always dominate it by another smooth projective variety that lifts to characteristic 0? We give a negative answer to this question.
Jason Lo (Cal State Northridge)
October 27, 2017
The effect of Fourier-Mukai transforms on slope stability on elliptic fibrations
Slope stability is a type of stability for coherent sheaves on smooth projective varieties. On a variety where the derived category of coherent sheaves admits a non-trivial autoequivalence, it is natural to ask how slope stability `transforms’ to a different stability under the autoequivalence. This question also has implications for understanding the symmetries within various counting invariants. In this talk, we will give an answer to the above question for elliptic surfaces and threefolds under a Fourier-Mukai transform.
Daniel Litt (Columbia University)
December 1, 2017
Galois actions on fundamental groups
Let X be a variety over a field k, and let x be a k-rational point of X. Then the absolute Galois group of k acts on the etale fundamental group of X. If k is an arithmetically interesting field (i.e. a number field, a p-adic field, or a finite field), then this action reveals a great deal about the geometry of X; if X is a variety with an interesting fundamental group, this action reveals a great deal about the arithmetic of k.
This talk will discuss (1) joint work with Alexander Betts about the structure of Galois actions on fundamental groups, (2) how to describe invariants of these actions in terms of more geometric invariants of X, and (3) applications of this work to classical algebraic geometry, and, if time permits, arithmetic.
Pablo Solis (Stanford)
January 19, 2018
Hunting Vector Bundles on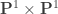 
Motivated by Boij-Soderberg theory, Eisenbud and Schreyer conjectured there should be vector bundles on 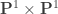with natural cohomology and prescribed Euler characteristic. I’ll give some background on Boij-Soderberg theory, explain what natural cohomology means and prove the conjecture in “most” cases.
Izzet Coskun (University of Illinois at Chicago)
January 26, 2018
The geometry of moduli spaces of sheaves on surfaces
In this talk, I will discuss recent results concerning the Brill-Noether Theory of higher rank bundles on rational surfaces and stable cohomology of moduli spaces of sheaves. In joint work with Jack Huizenga, we characterize when the cohomology of a general stable sheaf on a Hirzebruch surface is determined by its Euler characteristic. We use these results to classify moduli spaces where the general bundle is globally generated. If time permits, I will discuss joint work with Matthew Woolf on the stable cohomology of moduli spaces on rational surfaces.
Katrina Honigs (Utah)
February 2, 2018
Fourier-Mukai partners of Enriques and bielliptic surfaces in positive characteristic
There are many results characterizing when derived categories of two complex surfaces are equivalent, including theorems of Bridgeland and Maciocia showing that derived equivalent Enriques or bielliptic surfaces must be isomorphic. The proofs of these theorems strongly use Torelli theorems and lattice-theoretic methods which are not available in positive characteristic. In this talk I will discuss how to prove these results over algebraically closed fields of positive characteristic (excluding some low characteristic cases). This work is joint with M. Lieblich and S. Tirabassi.
Junliang Shen (ETH)
February 9, 2018
K3 categories, cubic 4-folds, and the Beauville-Voisin conjecture
We discuss recent progress on the connection between 0-cycles of holomorphic symplectic varieties and structures of K3 categories. We propose that there exists a sheaf/cycle correspondence for any K3 category, which controls the geometry of algebraically coisotropic subvarieties of certain holomorphic symplectic varieties. Two concrete cases will be illustrated in details:
(1) the derived category of a K3 surface (joint with Qizheng Yin and Xiaolei Zhao),
(2) Kuznetsov category of a cubic 4-fold (joint with Qizheng Yin).
If time permits, we will also discuss the connection to rational curves in cubic 4-folds.
Michael Viscardi (Berkeley)
February 16, 2018
Quantum cohomology and 3D mirror symmetry
Recent work on equivariant aspects of mirror symmetry has discovered relations between the equivariant quantum cohomology of symplectic resolutions and Casimir-type connections (among many other objects). We provide a new example of this theory in the setting of the affine Grassmannian, a fundamental space in the geometric Langlands program. More precisely, we identify the equivariant quantum connection of certain symplectic resolutions of slices in the affine Grassmannian of a semisimple group G with a trigonometric Knizhnik-Zamolodchikov (KZ)-type connection of the Langlands dual group of G. These symplectic resolutions are expected to be symplectic duals of Nakajima quiver varieties, so that our result is an analogue of (part of) the work of Maulik and Okounkov in the symplectic dual setting.
Roya Beheshti (Washington U. St. Louis)
February 23, 2018
Moduli spaces of rational curves on hypersurfaces
I will talk about the geometry of moduli spaces of rational curves on Fano hypersurfaces and discuss some results concerning their dimension and birational geometry.
Yongbin Ruan (Michigan)
March 9, 2018
The structure of higher genus Gromov-Witten invariants of quintic 3-fold
The computation of higher genus Gromov-Witten invariants of quintic 3–fold (or compact Calabi-Yau manifold in general) has been a focal point of research of geometric and physics for more than twenty years. A series of deep conjectures have been proposed via mirror symmetry for the specific solutions as well as structures of its generating functions. Building on our initial success for a proof of genus two conjecture formula of BCOV, we present a proof of two conjectures regarding the structure of the theory. The first one is Yamaguchi-Yau’s conjecture that its generating function is a polynomial of five generators and the other one is the famous holomorphic anomaly equation which governs the dependence on four out of five generators. This is a joint work with Shuai Guo and Felix Janda.
Andrei Calderaru (Wisconsin)
April 13, 2018
Computing a categorical Gromov-Witten invariant
In his 2005 paper “The Gromov-Witten potential associated to a TCFT” Kevin Costello described a procedure for recovering an analogue of the Gromov-Witten potential directly out of a cyclic A-inifinity algebra or category. Applying his construction to the derived category of sheaves of a complex projective variety provides a definition of higher genus B-model Gromov-Witten invariants, independent of the BCOV formalism. This has several advantages. Due to the categorical invariance of these invariants, categorical mirror symmetry automatically implies classical mirror symmetry to all genera. Also, the construction can be applied to other categories like categories of matrix factorization, giving a direct definition of FJRW invariants, for example.
In my talk I shall describe the details of the computation (joint with Junwu Tu) of the invariant, at g=1, n=1, for elliptic curves. The result agrees with the predictions of mirror symmetry, matching classical calculations of Dijkgraaf. It is the first non-trivial computation of a categorical Gromov-Witten invariant.
Daniel Halpern-Leistner (Cornell)
April 20, 2018
What is wall-crossing?
I will discuss recent progress in understanding geometric invariant theory from an “intrinsic” perspective. This leads to a conceptually clean meta-principle for how to study the birational geometry of moduli spaces as well as a universal wall-crossing formula for the integrals of tautological K-theory classes on these moduli spaces. I will apply this perspective to the example of Bridgeland semistable complexes on an algebraic surface. The result is a relatively straightforward construction of K-theoretic Donaldson invariants, along with wall-crossing formulas for these invariants which are new-ish (conjecturally equivalent to Mochizuki’s cohomological wall crossing formulas in the context where both are defined).
Sean Howe (Stanford)
April 27, 2018
Motivic random variables and random matrices
As first shown by Katz-Sarnak, the zero spacing of L-functions of smooth plane curves over finite fields approximate the infinite random matrix statistics observed experimentally for the zero spacing of the Riemann-Zeta function (arbitrarily well by first taking the size of the finite field to infinity, and then the degree of the curve to infinity). The key geometric inputs are a computation of the image of the monodromy representation and Deligne’s purity theorem, which ensures that only the zeroth cohomology group of irreducible local systems will contribute asymptotically to the statistics. In this talk, we explain how higher order terms (i.e. the lower weight part of cohomology) can be computed starting from a simple heuristic for the number of points on a random smooth plane curve.
Isabel Vogt (MIT)
May 4, 2018, 3-4 pm
Interpolation problems for curves in projective space
In this talk we will discuss the following question: When does there exist a curve of degree 
and genus 
passing through 
general points in 
?
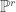Eric Larson (MIT)
May 4, 2018, 4:30-5:30 pm
The Maximal Rank Conjecture
We find the Hilbert function of a general curve of genus , embedded in 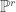via a general linear series of degree . Note that Isabel Vogt’s talk earlier this afternoon is a pre-requisite for this talk.
Dori Bejleri (Brown)
May 18, 2018, 3-4 pm
Stable pair compactifications of the moduli space of degree one del Pezzo surfaces via elliptic fibrations
A degree one del Pezzo surface is the blowup of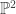 
at 8 general points. By the classical Cayley-Bacharach Theorem, there is a unique 9th point whose blowup produces a rational elliptic surface with a section. Via this relationship, we can construct a stable pair compactification of the moduli space of anti-canonically polarized degree one del Pezzo surfaces. The KSBA theory of stable pairs $(X,D)$ is the natural extension to dimension 2 of the Deligne-Mumford-Knudsen theory of stable curves. I will discuss the construction of the space of interest as a limit of a space of weighted stable elliptic surface pairs and explain how it relates to some previous compactifications of the space of degree one del Pezzo surfaces. This is joint work with Kenny Ascher.
Francois Greer (Stony Brook)
May 18, 2018, 4:30-5:30 pm
Elliptic fibrations in the presence of singularities
The Gromov-Witten generating series for an elliptic fibration is expected to have modular properties by mirror symmetry. When the homology class in the base is irreducible and the total space is smooth, we obtain a classical modular form for the full modular group. If the base class is reducible, we expect the series to be quasi-modular. If the fibration does not admit a section, then the modular form has higher level. Both of these relaxations are related to the presence of singularities in the geometry.
Soren Galatius (Stanford)
May 25, 2018, 3-4 pm, Room TBA
, 
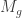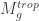, GRT, and Kontsevich’s complex of graphs
I will report on recent joint work with Melody Chan and Sam Payne on the cohomology of 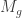in degree 
. It is known that the rational cohomology vanishes above this degree. We prove that the rational cohomology in this degree is non-trivial for all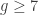 
and that its dimension grows faster than 
constant, making it asymptotically larger than the entire tautological ring and disproving a recent conjecture of Church-Farb-Putman and an older conjecture of Kontsevich. Our proof relates the weight filtration on compactly supported cohomology of 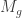with the moduli space of tropical curves and with the cohomology of Kontsevich’s graph complex. We then use a theorem of Willwacher to construct an injection of the Grothendieck-Teichmüller Lie algebra into 
.
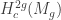Tathagata Basak (Iowa State University)
May 25, 2018, 4:30-5:30 pm
A complex ball quotient and the monster
We shall talk about an arithmetic lattice M in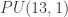 
acting on the the unit ball B in thirteen dimensional complex vector space. Let X be the space obtained by removing the hypersurfaces in B that have nontrivial stabilizer in M and then quotienting the rest by M. The fundamental group G of the ball quotient X is a complex hyperbolic analog of the braid group. We shall state a conjecture that relates this fundamental group G and the monster simple group and describe our results (joint with D. Allcock) towards this conjecture.
The discrete group M is related to the Leech lattice and has generators and relations analogous to Weyl groups. Time permitting, we shall give a second example in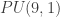 
related to the Barnes-Wall lattice for which there is a similar story.
Algebraic Geometry at Stanford 